Chapter 1 – Problem Solving with Math 141. Multiply (round solution to nearest hundredth): 9.158 14.382 142. Divide (round to nearest tenth): 118,000 3.95 143. Complete by shortcut method: 43.81 1,000 144. Complete by shortcut method: 11,896.413 1,000 145. Complete by shortcut method: 3,069.44 1,000 146. Mel Doane is taking his office staff. Useful solutions for standard problems Preface Modelling is a key part of design. In the early stage, approximate modelling establishes whether the concept will work at all, and identifies the combination of material properties that maximize performance. Pythagorean Triples 106. Cutting Regions 112. Counting Triangles 124. Counting Rectangles 133. Balls and Boxes 147. Clock Problems 165. Page Numbers 176. Finding Minimum Maximum Values with Inequalities 185. Diverse group is the best solution for problem-solving tasks By Jared Wadley News Service. A diverse group of problem solvers is more likely to outperform a team of the best and brightest problem solvers, a U-M study shows. Individuals chosen from a diverse, randomly selected pool will offer different perspectives that could result in better.

Chapter Round Materialmath Problem Solving Inequalities

• 2.1: Taking Measurements

  Chemists measure the properties of matter and express these measurements as quantities. A quantity is an amount of something and consists of a number and a unit. The number tells us how many (or how much), and the unit tells us what the scale of measurement is. For example, when a distance is reported as “5 kilometers,” we know that the quantity has been expressed in units of kilometers and that the number of kilometers is 5.

• 2.2: Scientific Notation - Writing Large and Small Numbers

  Chemists often work with numbers that are exceedingly large or small. For example, entering the mass in grams of a hydrogen atom into a calculator requires a display with at least 24 decimal places. A system called scientific notation avoids much of the tedium and awkwardness of manipulating numbers with large or small magnitudes.

• 2.3: Significant Figures - Writing Numbers to Reflect Precision

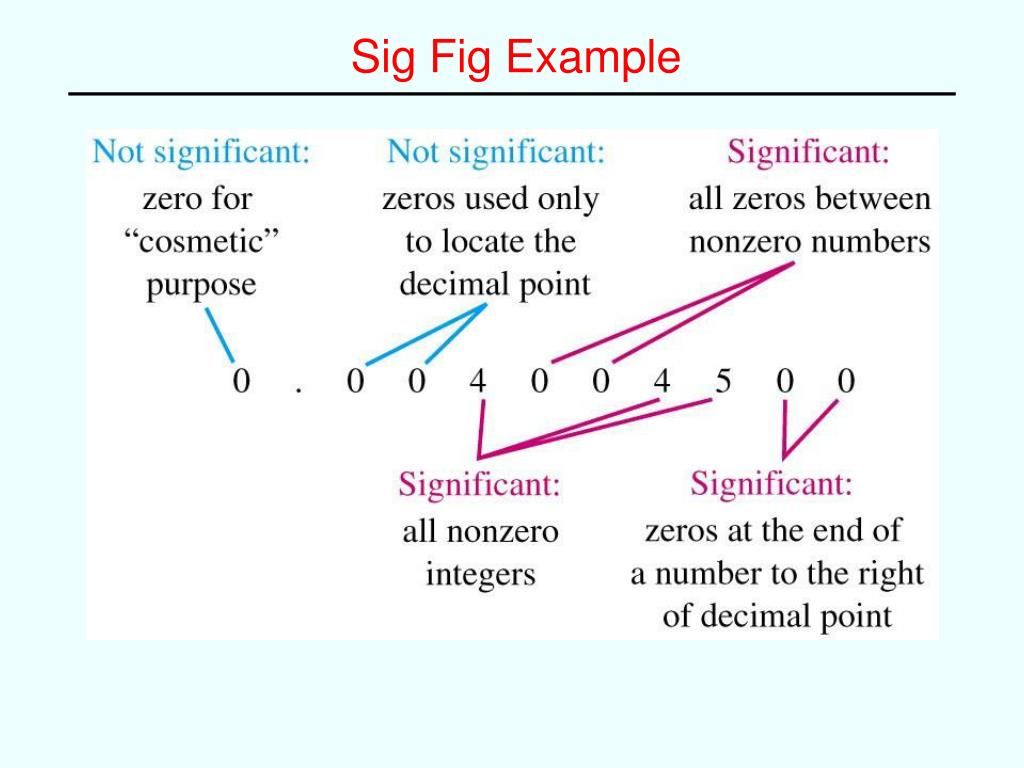
  Uncertainty exists in all measurements. The degree of uncertainty is affected in part by the quality of the measuring tool. Significant figures give an indication of the certainty of a measurement. Rules allow decisions to be made about how many digits to use in any given situation.

• 2.4: Significant Figures in Calculations

  To round a number, first decide how many significant figures the number should have. Once you know that, round to that many digits, starting from the left. If the number immediately to the right of the last significant digit is less than 5, it is dropped and the value of the last significant digit remains the same. If the number immediately to the right of the last significant digit is greater than or equal to 5, the last significant digit is increased by 1.

• 2.5: The Basic Units of Measurement

  Metric prefixes derive from Latin or Greek terms. The prefixes are used to make the units manageable. The SI system is based on multiples of ten. There are seven basic units in the SI system. Five of these units are commonly used in chemistry.

• 2.6: Problem Solving and Unit Conversions

  During your studies of chemistry (and physics also), you will note that mathematical equations are used in a number of different applications. Many of these equations have a number of different variables with which you will need to work. You should also note that these equations will often require you to use measurements with their units. Algebra skills become very important here!

• 2.7: Solving Multistep Conversion Problems

  Sometimes you will have to perform more than one conversion to obtain the desired unit.

• 2.8: Units Raised to a Power

  Conversion factors for area and volume can also be produced by the dimensional analysis method. Just remember that if a quantity is raised to a power of 10 both the number and the unit must be raised to the same power of 10.

• 2.9: Density

  Density is a physical property found by dividing the mass of an object by its volume. Regardless of the sample size, density is always constant.

• 2.E: Homework Chapter 2

• 2.E: Homework Chapter 2 Answers